Sorting of data is one of the most fundamental, yet important problem in computer science. Sorting forms a great case study for those who want to learn Data Structures and Algorithms.
What is Sorting - Definition
Often in real life, we are supposed to arrange data in a particular order. For instance, during our school days, we are told to stand in the queue based on our heights. Another example is the attendance register at school/college which contains our names arranged in alphabetical order.
These data arrangements give easier access to data for future use for ex. finding "Joe" in an attendance register of 100 students. The arrangement of data in a particular order is called as sorting of the data by that order. 2 of the most commonly used orders are:
- Ascending order: while sorting the data in ascending order, we try to arrange the data in a way such that each element is in some way “smaller than” its successor. This “smaller than” relation is an ordered relation over the set from which the data is taken. As a simple example, the numbers 1, 2, 3, 4, 5 are sorted in ascending order. Here, the “smaller than” relation is actually the “<” operator. As can be seen, 1 < 2 < 3 < 4 < 5.
- Descending order: descending order is the exact opposite of ascending order. Given a data that is sorted in ascending order, reverse it and you will get the data in descending order.
Due to the similar nature of the 2 orders, we often drop the actual order and we say - we want to sort the data. This generally means that we want the data to be sorted in ascending order. Before we get into the details of the sorting algorithm, let us understand the problem statement.
Problem statement
We are given an array (or a list) of data. We are also given a way to “order” the elements present in the data. Now, we are asked to arranged the data as per the given order. As an example, we are given an array of integers: [5, 1, 4, 2, 3]. We are given the “order” as “smaller than”. So, we are asked to arrange the elements of this array in such a way that each element is smaller than its successor. Basically, we need to find a way to sort this array so that the final array obtained is [1, 2, 3, 4, 5]. There are several techniques/algorithms to achieve this ordered output array. One such well-known technique that we will discuss in this blog is called Bubble Sort.
Bubble Sort Algorithm in C - Introduction
Bubble Sort in C is a sorting algorithm where we repeatedly iterate through the array and swap adjacent elements that are unordered. We repeat this until the array is sorted.
As an example, for the array mentioned above - [5, 1, 4, 2, 3] we can see that 5 should not be on the left of 1 and so, we swap them to get: [1, 5, 4, 2, 3]. Next, we see that 5 should again not be on the left of 4. We swap 5 and 4 to get [1, 4, 5, 2, 3]. We repeat this for 5 and 2 and subsequently for 5 and 3 to get [1, 4, 2, 3, 5].
As can be seen - after one “pass” over the array, the largest element (5 in this case) has reached its correct position - extreme right. Let us try to repeat this process.
(1, 4) is correct. However, (4, 2) is an incorrect order. Therefore, we swap 4 and 2 to get [1, 2, 4, 3, 5]. Now again, (4, 3) is incorrect so we do another swap and get [1, 2, 3, 4, 5].
As can be seen, the array is sorted!
This exactly is how bubble sort in C works.
As an example, check this graphic that pictorially depicts how bubble sort works.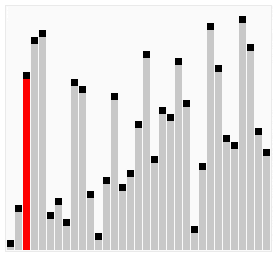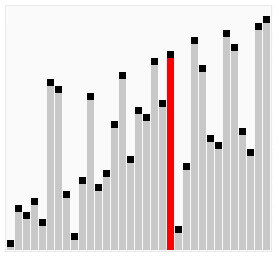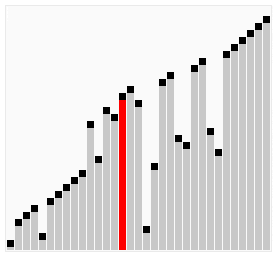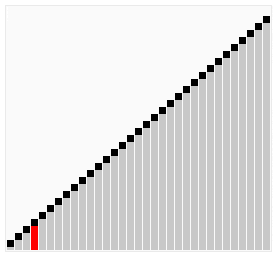
Suggested Course
Master the Coding Interview: Data Structures + Algorithms
Bubble Sort - Explanation
In the first “pass” through the array, the largest element will always get swapped until it is placed to the extreme right. This is because this largest element will always break the desired order. So, at the end of the first pass, the largest element will always reach its correct position.
Now that the largest element has reached its correct position (for instance, 5 reached the last position), we can simply ignore it and concentrate on the rest of the array ([1, 4, 2, 3] in the above case). Here, the largest element in the rest of the array (which is 4) will be nothing but the second largest element in the array. By the above recursive argument, this second largest array will then reach the last position in the remaining array ([1, 2, 3, 4]). This is nothing but a recursive argument on the remaining array.
This continues until for n iterations where n = number of elements in the array. Finally, the array gets sorted.
#include <stdio.h>
void bubble_sort(int a[], int n) {
int i = 0, j = 0, tmp;
for (i = 0; i < n; i++) { // loop n times - 1 per element
for (j = 0; j < n - i - 1; j++) { // last i elements are sorted already
if (a[j] > a[j + 1]) { // swop if order is broken
tmp = a[j];
a[j] = a[j + 1];
a[j + 1] = tmp;
}
}
}
}
int main() {
int a[100], n, i, d, swap;
printf("Enter number of elements in the array:\n");
scanf("%d", &n);
printf("Enter %d integers\n", n);
for (i = 0; i < n; i++)
scanf("%d", &a[i]);
bubble_sort(a, n);
printf("Printing the sorted array:\n");
for (i = 0; i < n; i++)
printf("%d\n", a[i]);
return 0;
}
Bubble Sort Program in C
We loop n times - once for each element of the array. When i = 0, with the j loop, the largest element of the array reaches its correct position. When i = 1, with the j loop, the second largest element of the array reaches its correct position. So on and so forth.
Conclusion
Bubble sort is a fairly simple algorithm. It forms an interesting example of how simple computations can be used to perform more complex tasks. However, there is one issue with the algorithm - it is relatively slower compared to other sorting algorithms. To understand that, let us take a look at the loops involved - there are 2 loops:
- First, the outer loop of variable i that goes from i = 0 to i = n - 1.
- For each iteration of the outer i loop, the inner loop of variable j goes from j = 0 to j = n - i - 2.
We can consolidate the number of iterations to see that:
- When i = 0, the inner j loop goes from j = 0 to j = n - 2
- When i = 1, the inner j loop goes from j = 0 to j = n - 3
- When i = 2, the inner j loop goes from j = 0 to j = n - 4
- When i = n - 2, the inner j loop goes from j = 0 to j = 0
We can sum this up to see that the total iterations are (n - 2) + (n - 3) + (n - 4) … + 1 + 0 = (n - 2) * (n - 3) / 2 = (n2 - 5n + 6) / 2 = n2/2 - 2.5n + 3As can be seen, this term is proportional to n2 (the largest power of n is n2). Mathematically, this is stated as - bubble sort algorithm is of O(n2) complexity. This isn’t the best because when n is large (say n = 106), n2 is huge (n2 = 1012). Therefore, it will take a lot of iterations for the algorithm to complete. This is undesirable. There are some better algorithms like merge sort in C, etc that take O(nlog2n) iterations. logn is much smaller than n. As an example, when n = 230 (which is approximately 109), log2n is just 30). Nevertheless, bubble sort is an interesting algorithm and is a great way for beginners to understand how sorting works.
People are also reading:
